Minimization Problem

End goal :
Suppose \(A \in \mathcal{L}(\mathcal{R}^n, \mathcal{R}^m)\) and \(b \in \mathcal{L}(\mathcal{R}^m)\). Find \(x \in \mathcal{L}(\mathcal{R}^n)\) to get \(min \|b - Ax\|\).

Explore eigenvectors of \(A^TA\) and \(AA^T\)

\(\left(A^TA\right)^T = A^TA\) shows that \(A^TA\) is self-adjoint (and also positive). Thus \(\mathcal{R}^n\) has an orthonormal basis consisting of eigenvectors of \(A^TA\):

\[A^TA(v_1,\cdots,v_r,v_{r+1},\cdots,v_n) = (\lambda_1 v_1,\cdots,\lambda_r v_r,0v_{r+1},\cdots,0v_n)\]

Now explore the vector \(Av_i\).

\[(Av_i)^T(Av_j)=v^T_i A^T A v_j = \lambda_j v^T_i v_j = \lambda_j \mbox{ or } 0\]

If i > r, \(\|Av_i\|^2 = 0 \rightarrow Av_i=0\)
If i <= r, \(\|Av_k\|^2 = \lambda_i \gt 0 \rightarrow \|Av_i\|=\sqrt{\lambda_i}\)
Suppose

\(u_i = \frac{Av_i}{\|Av_i\|}=\frac{Av_i}{\sqrt{\lambda_i}}=\frac{Av_i}{\sigma_i}\) .

We get an orthonormal list \((u_1, \cdots, u_r)\). It is an orthonormal basis of \(range A\):

\[\begin{align*} x & = a_1 v_1 + \cdots + a_r v_r + a_{r+1} v_{r+1} + \cdots + a_n v_n \\ Ax & = a_1Av_1 + \cdots + a_rAv_r + 0 + \cdots + 0 \\ & = a_1 \sigma_1 u_1 + \cdots + a_r \sigma_r u_r \end{align*}\]

We also get an orthonormal basis of \(null A\): \((v_{r+1},\cdots, v_n)\).

And because \(null A^\ast = (range A)^\bot\) and \(null A = (range A^\ast)^\bot\), we have that:

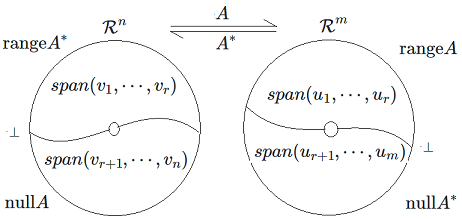
The following equation shows that the column space of M(A) is \(\mbox{range} A\):

\[Ax = \begin{bmatrix} C_1 & C_2 & \cdots & C_n \end{bmatrix} x\]

The following equation shows that the row space of M(A) is \((\mbox{null} A)^\bot\).

\[Ax = \begin{bmatrix} A_1 \\ A_2 \\ \vdots \\ A_m \end{bmatrix} x = 0\]

Explore the relationship of eigenvectors of \(A^TA\) and eigenvectors of \(AA^T\). For i = 1,2,…, r:

\[\begin{align*} A^TAv_i=\lambda_iv_i & \Rightarrow AA^TAv_i=\lambda_iAv_i \\ & \Rightarrow AA^T\sigma_iu_i=\lambda_i\sigma_iu_i \\ & \Rightarrow AA^Tu_i=\lambda_iu_i \\ \end{align*}\]

Thus \((u_1,\cdots,u_r)\) is orthogonal eigenvectors of \(AA^T\). Extend it to orthonormal basis of \(\mathcal{R}^m\): \((u_1,\cdots,u_r,u_{r+1},\cdots,u_m)\) which are orthonormal eigenvectors of \(AA^T\).

Orthogonal Projection for Minimization Problem

We can solve the minimization problem by finding the orthogonal projection of b.

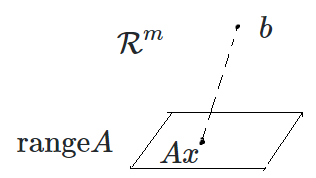
If \(Ax=P_Ub \,(U = \mbox{range} A)\), we get the min: \(min\|b-Ax\|=\|P_{U^\bot}b\|\). Because

\[\begin{align*} Ax & = a_1\sigma_1u_1 + \cdots + a_r\sigma_ru_r \\ P_Ub & = \langle b, u_1 \rangle u_1 + \cdots +\langle b, u_r \rangle u_r \end{align*}\]

Thus,

\[\begin{align*} Ax = P_Ub & \Rightarrow a_i\sigma_i = \langle b, u_i \rangle \\ & \Rightarrow a_i = \frac{u_i^Tb}{\sigma_i} \end{align*}\]

Thus we have

\[\begin{align*} x & = \sum_{i=1}^r \frac{u_i^Tb}{\sigma_i}v_i \\ min\|b-Ax\|^2 &= \|P_{U^\bot} b\|^2 = \sum_{i=r+1}^m(u_i^Tb)^2 \end{align*}\]

Singular Value Decomposition (SVD)

We can also solve the issue via SVD.

Construct matrix of \(T \in \mathcal{L}(\mathcal{R}^n)\) with standard basis:

\[M(T,(e_1,\cdots,e_n)) = \begin{bmatrix} v_1 & \cdots & v_n \end{bmatrix}\]

And matrix of \(T^\ast \in \mathcal{L}(\mathcal{R}^n)\) with standard basis will be:

\[M(T^\ast,(e_1,\cdots,e_n)) = \begin{bmatrix} v_1^T \\ \vdots \\ v_n^T \end{bmatrix}\]

We’ll explore the property of the linear map \(T\) and \(T^\ast\).

\[\begin{align*} x & = a_1v_1 + \cdots + a_nv_n \\ T^\ast x & = a_1T^\ast v_1 + \cdots + a_nT^\ast v_n \\ & = a_1e_1 + \cdots + a_ne_n \\ \end{align*}\]

Thus \(\|T^\ast x\| = \|x\|\), in other words, \(T^\ast\) is an isometry. Thus we have

\[\begin{align*} T^\ast T & = TT^\ast = I \\ T^\ast & = T^{-1} \end{align*}\]

Now turn to SVD.

Suppose \((v_1,\cdots,v_n)\) is an orthonormal basis of \(A^TA \in \mathcal{L}({\mathcal{R}^n})\). And \((u_1,\cdots,u_m)\) is an orthonormal basis of \(AA^T \in \mathcal{L}({\mathcal{R}^m})\). Thus we get the Singular Value Decomposition:

\[A \begin{bmatrix} v_1 & \cdots & v_n \end{bmatrix} = \begin{bmatrix} u_1 & \cdots & u_m \end{bmatrix} \begin{bmatrix} \sigma_1 \\ & \ddots \\ & & \sigma_r \\ & & & 0 \\ & & & & \ddots \\ & & & & & 0 \\ \end{bmatrix}_{mn}\]

We can write it in matrix form: \(AV=U\Sigma\) or \(A=U\Sigma V^T\)

How to get min of \(\|b - A_{mn}x\|\) ?

\[\begin{align*} \|b-Ax\| & = \|U^T(b-Ax)\| \\ & = \|U^Tb-U^TAx\| \\ & = \|U^Tb-\Sigma V^Tx\| \\ & = \|U^Tb-\Sigma z\| \\ \|b-Ax\|^2 & = \sum_{i=1}^r(u_i^Tb-\sigma_iz_i)^2 + \sum_{i=r+1}^m(u_i^Tb)^2 \end{align*}\]

To get \(min \|b-Ax\|\), we need the first term equal 0, in other words, \(z_i=\frac{u_i^Tb}{\sigma_i}\). From \(V^Tx=z\), we get

\[x = Vz = \begin{bmatrix}v_1 & \cdots & v_n \end{bmatrix} \begin{bmatrix} \frac{1}{\sigma_1}u_1^Tb \\ \vdots \\ \frac{1}{\sigma_r} u_r^Tb\\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^r \frac{1}{\sigma_i}u_i^Tbv_i\]

(With a matrix form: \(x = V{\Sigma}^{+} U^Tb\))

Thus we have

\[min\|b-Ax\|^2 = \sum_{i=r+1}^m(u_i^Tb)^2\]

Normal Equation

If the matrix A is invertible, we can solve the issue with Normal Equation:

\[\hat x = (A^TA)^{-1} A^T b\]