Cross Validation

Cross-Validation plays an important role in model selection and model fine-tuning. We will go through the whole process to show how cross-validation works. The following topics will be discussed:

cross-validation for overfitting issue
cross-validation for model selection
cross-validation for model fine-tuning

Underfitting and Overfitting issue

Suppose we have prepared the data for training and we will try the linear model at first. The “prepare data” code was showed in the Pipeline page.

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)

To evaluate the regression model, we can take the root mean square error (RMSE) as the performance measure metric. Check the regression model’s RMSE on the whole training set:

from sklearn.metrics import mean_squared_error

housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
Out[7]: 68628.19819848922

It’s not a good score: most median_housing_values range between $120,000 and $256,000. The model underfits the training data. It happens when the features do not provide enough information to make a good prediction, or when the model is not powerful enough.

Let’s try a more powerful model to resolve the underfitting issue. Suppose we try the decision tree model:

from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor(random_state=42)
tree_reg.fit(housing_prepared, housing_labels)

housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
Out[12]: 0.0

The underfitting issue is resolved. And it seems this model is absolutely perfect. However, it is much more likely that the model has badly overfits the training data. To check whether there is an overfitting issue, we can make use of cross-validation introduced in Split Data Set page: split the training set into two part, train the model with one part (smaller training set) and evaluate the performance with the other part (validation set).

Cross Validation for Model Selection

Scikit-Learn provides a K-fold cross-validation feature. The following code randomly splits the training set into 10 distinct subsets called folds, then each time it picks a different fold for evaluation and trains the model with the other 9 folds. Thus it trains and evaluates the model 10 times. The result is an array containing 10 evaluation scores.

from sklearn.model_selection import cross_val_score

scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
                         scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-scores)

def display_scores(scores):
    print("Scores:", scores)
    print("Mean:", scores.mean())
    print("Standard deviation:", scores.std())

display_scores(tree_rmse_scores)

Scores: [70194.33680785 66855.16363941 72432.58244769 70758.73896782
 71115.88230639 75585.14172901 70262.86139133 70273.6325285
 75366.87952553 71231.65726027]
Mean: 71407.68766037929
Standard deviation: 2439.4345041191004

The scores shows that Decision Tree Model indeed overfits the training data, it performs badly on the validation sets while performs perfectly on the training set.

Let’s try different models to shortlist a few promising models. And then fine-tune these promising models to get a better one. The following is the result of several models:

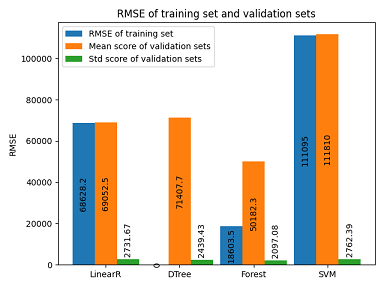
RMSE Compare

Linear Regression and SVM perform badly on both sets – severe underfitting. Decision Tree performs perfectly on training set whereas badly on validation sets – severe overfitting. Among these models, Random Forest is the best one. However, it still overfits the training data. We can fine-tune the model so that it performs better.