05 Backpropagation

There’s one thing we did not talk about: how to calculate the partial derivatives? In other words, how to calculate \(\frac{\partial C_{X_i}}{\partial w}\) for the “step” function:

\begin{eqnarray} w & \rightarrow & w’ = w-\frac{\eta}{n} \sum_j \frac{\partial C_{X_i}}{\partial w} \end{eqnarray}

I will discuss how to calculate in this class. First begin with some convention:

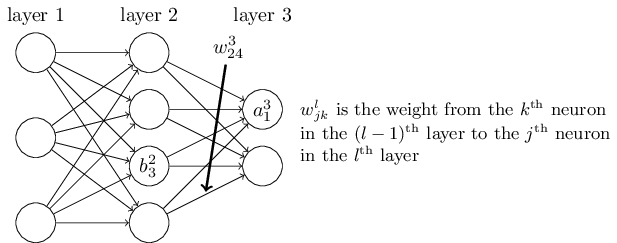
From the digram, we know the meaning of \(w^{l}_{jk}, \; a^{l}_j, \; b^{l}_j\). Besides, we have the formula:

\[a^l_j = \sigma\left(z^l_j \right) \; and \; z^l_j = \sum_k w^{l}_{jk} a^{l-1}_k + b^l_j\]

Take the the vectorized form: \(a^l = \sigma(z^l) \; and \; z^l \equiv w^l a^{l-1}+b^l\)

Note: \(a^l_j\) is the output of the \(j^{th}\) neuron in layer l and some article makes use of other symbols instead, for example: \(o^l_j\).

Deriving the Gradients

The reader shall have the math foundation of partial derivatives and partial derivatives of multivariate functions. Here is the derivation:

\[\begin{equation*} \begin{split} \frac{\partial C}{\partial w^l_{jk}} & = \frac{\partial C}{\partial z^l_j} \cdot \frac{\partial z^l_j}{\partial w^l_{jk}} \\ & = \delta^l_j \cdot \frac{\partial}{\partial w^l_{jk}} \left( \sum_m w^l_{jm} a^{l-1}_m + b^l_j \right) \\ & = \delta^l_j \cdot a^{l-1}_k \end{split} \end{equation*}\]

and:

\[\begin{equation*} \begin{split} \delta^l_j = \frac{\partial C}{\partial z^l_j} & = \sum_m \frac{\partial C}{\partial z^{l+1}_m} \cdot \frac{\partial z^{l+1}_m}{\partial z^l_j} \\ & = \sum_m \delta^{l+1}_m \cdot \frac{\partial}{\partial z^l_j} \left( \sum_n w^{l+1}_{mn} \sigma \left(z^l_n \right) + b^{l+1}_m \right) \\ & = \sum_m \delta^{l+1}_m \cdot w^{l+1}_{mj} \cdot \sigma'(z^l_j) \\ & = \sigma'(z^l_j) \cdot \sum_m \delta^{l+1}_m w^{l+1}_{mj} \end{split} \end{equation*}\]

The sigmoid function has a good property: its derivative is simple:

\[\sigma'(z) = \sigma(z) (1 - \sigma(z))\]

It simplifies the calculation of derivatives: just reuse the output of the neuron: \(a^l_j\) that was calculated from the forward phrase:

\[\begin{equation*} \delta^l_j = a^l_j \cdot (1 - a^l_j) \cdot \sum_m \delta^{l+1}_m w^{l+1}_{mj} \end{equation*}\]

The backpropagation algorithm

For each example \(X_i\), calculate its partial derivatives (by the following algrithms). After consuming all the examples, we get the step listed in the beginning of the page.

1. Feedforward: For each l=2,3,…,L compute

   \[z^{l} = w^l a^{l-1}+b^l \; \mbox{and} \; a^{l} = \sigma(z^{l})\]

2. Output error \(\delta^L\): Compute the vector

   \[\delta^{L} = \nabla_a C \odot \sigma'(z^L)\]

3. Backpropagate the error: For each l=L−1,L−2,…,2 compute:

   \[\delta^{l} = a^l \odot (1 - a^l) \odot ((w^{l+1})^T \delta^{l+1})\]

4. Output: The gradient of the cost function is given by

   \[\frac{\partial C_{X_i}}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \; \mbox{and} \; \frac{\partial C_{X_i}}{\partial b^l_j} = \delta^l_j\]