03 Some Thought on Neural Nets/Network
We have already shown how a neural net works in deep learning. But there’re some issues with the model and the algrithm. We’ll disscuss more on that. Some of the questions, I have no idea currently. But I will have an investigation after some time.
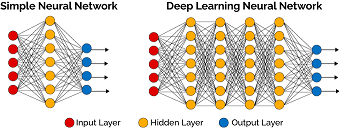
layers in neural networks
Let’s go back to the problem to resolve: recognize handwritten digits.
Suppose one image contains only one digit and the image has 28 x 28 pixels.
A simple design is that: there’re 784 inputs and 10 output in the network.
We can say that the network contains two layers: input layer and output layer.
There’re w with dim of 10 x 784 and b with dim of 10 to be resolved.
It works but not with a high performance. Engineers’d like to add some “hidden” layers to get a good performance. It seems more layers works better than 2-layers networks. Why? It’s question to discuss in the future.
cost function
From the previous discussion, we will use a quadratic cost function \(\frac{1}{2n} \sum_x \| y(x) - \hat{y}\|^2\). It is usually called Mean Square Error MSE. Why not use the form of Mean Absolute Error MAE:\(\frac{1}{n} \sum_x \| y(x) - \hat{y}\|\), or some other forms?
Let’s disscuss it in the future.
stochastic gradient descent
We have given the step equation for the point (w, b) so that it
walks towards the point that has smallest cost value. With the
training data, the \(\nabla C\) are calculated. It works when the training
data set is small. But deep learning needs plenty of training
data for a good performance. Thus the algrithm will work but
very slow. And speed may be not accepted in some situation.
How to speed up the process? stochastic gradient descent is a good idea. It just pick a small set of training data for training. Just call the small set the “mini-batch”. The idea is to estimate the gradient \(\nabla C\) by computing \(\nabla C_x\) for a small sample of randomly chosen training inputs. By averaging over this small sample it turns out that we can quickly get a good estimate of the true gradient \(\nabla C\), and this helps speed up gradient descent, and thus learning.
why can it work?