Conditional Probability and Independence
New evidence updates our beliefs or uncertainties about events. It leads to the concept of conditional probability. The situation where events provides on information about each other is called independence.
How to update beliefs with new evidence
We can get an intuition with a pebble world sample space. Recall that probablity behaves like mass. The following picture shows how to update the mass of an event A after observing new evidence B.
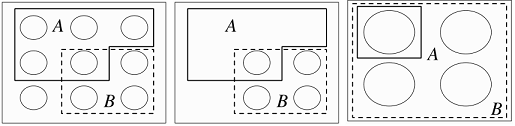
(a) Now suppose that we learn that B occurred.
(b) Upon obtaining this information, we get rid
of all the pebbles in \(B^c\) because
they are incompatible with the knowledge
that B has occurred. Then \(P(A\cap B)\) is the
total mass of the pebbles remaining in A.
(c) Finally, we renormalize, that is, divide
all the masses by a constant so that the
new total mass of the remaining pebbles
is 1. This is achieved by dividing by P(B),
the total mass of the pebbles in B.
The updated mass of the outcomes corresponding
to event A is \(P(A\cap B)/P(B)\).
In this way, probability of A (mass of the event A) have been updated in accordance with the observed evidence B.
Definition of Conditional Probability
If A and B are events with \(P(B)>0\), then the conditional probability of A given evidence B, denoted by \(P(A\mid B)\), is defined as
\[P(A\mid B)=\frac{P(A \cap B)}{P(B)}\]- \(P(A)\) is the prior probability of A (prior means before updating based on the evidence)
- \(P(A\mid B)\) is the posterior probability of A (posterior means after updating based on the evidence)