Integer Arithmetic Operation

Unsigned Integer Overflow

For an unsigned integer with 8-bits width, it ranges from 0 to 255. Consider the following code (via golang) and its output:

var a, b, c uint8 = 0x1, 0x2, 0xff
fmt.Println(a, b, c, a-b, a+c, b+c)
// Output:
//    1 2 255 255 0 1

What happened with the Arithmetic operation? Why 1-2 == 255?

We can observe similar things when watching the time. There’re 24 hours in two rounds in the clockface (in a day). Suppose it’s at one o’clock in the morning now. Here’re the questions:

what’s the time 2 hours earlier? — at 23 o’clock yesterday
what’s the time 23 hours later? — at 0 o’clock tomorrow

You see, 1-2 == 23 and 1+23 == 0. It can explain the phenomenon of unsigned integer overflow.

unsigned integer clockface

Here’s a video of unsigned integer overflow.

Complement Code & Integer Overflow

Before we discuss the integer overflow, we need to think about the concept of Complement Code.

As we know, the human-readable 2-bits representation of the integer 1 and -1:

1: 0000 0001
-1: 1000 0001

Add them together:

1 + (-1) => 0000 0001 + 1000 0001 => 1000 0001

The result is not 0. Why?

In fact, the computer uses complement code for Arithmetic operation.

to make the following work:

1 + (-1) = 0 ==> 0000 0001 + ???? ???? = 0000 0000
2 + (-2) = 0 ==> 0000 0010 + ???? ???? = 0000 0000
3 + (-3) = 0 ==> 0000 0011 + ???? ???? = 0000 0000

we get the complement code:

-1 : 1111 1111
-2 : 1111 1110
-3 : 1111 1101

Find the pattern (take -1 as an example) of origin code to complement code:

from negative integer:     -1
==> 2-bits representation: 1000 0001
==> absolute value:        0000 0001
==> one-complement:        1111 1110
==> add one:               1111 1111  -- the complement code

Thus we can get rule of the opposite side (take 1000 0001 as an example):

from complement code:    1000 0001
==> abstract 1:          1000 0000
==> one-complment:       0111 1111
==> change sign:         1111 1111    -- 2-bits representation
==> negative integer:    -127

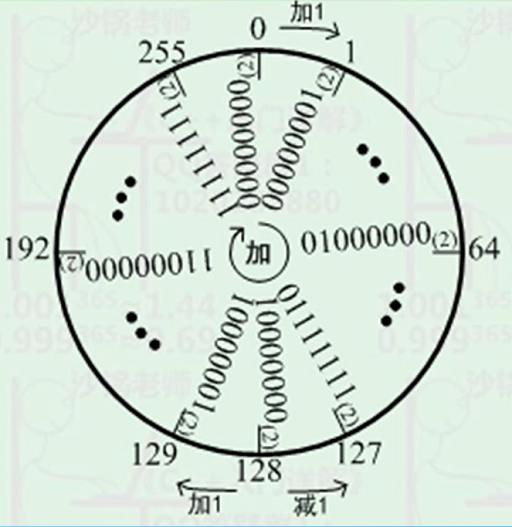
There’s a clockface for the integer arithmetic operation.

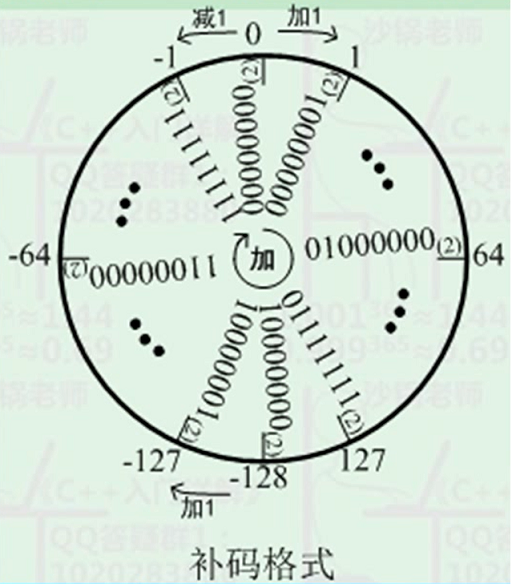
integer clockface

From the CPU’s point of view, it does not care about what is 1 or -1. It only concentrates on the machine code inside the circle. Increase a machine code by 1 will move clockwise by 1 step. Eventually, it will move to the origin - zero.

From a human’s point of view, there’re positive and negative integers with zero in the middle.

..., -3, -2, -1, 0, 1, 2, 3, ...

To make the arithmatic operation works as expected both in the cpu’s and human’s points of view, we relate each machine code (complement code) to a digit (as was shown in the picture).

Here’re related video (the above picture is from the latter video):

Complement Code, Interger Oveflow

After learning the above videos, can you explain the phenomenon of the integer overflow?

var d, e, f int8 = 0x1, 0x2, 0x7f
fmt.Println(d, e, f, d-e, d+f, e+f)
// Output:
//    1 2 127 -1 -128 -127