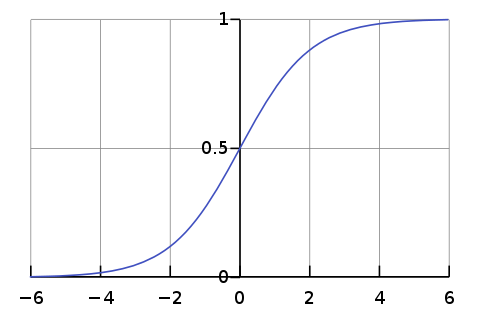
Neural Networks and Deep Learning

This is a tutorial about deep learning, the 2nd part of the ML series.

I will give basic underlying priciples and some intuition.

Lession 1 Neural Nets
Lession 2 Underlying Principles
Lession 3 Some Thought on Neural Nets/Network
Lession 4 Implementation
Lession 5 Backpropagation

Intro

From the Machine Learning Tutorial, we know that the ML app learns rules from examples automatically and create a classifier containing these rules. And then it can apply the rules on new input.

Deep learning is a model-based ML algrithm that works as follows: it adjusts its params so that the training data “works” on it — rules are learnt. Thus the model with the adjusted params contains rules from examples.

We will discuss the model in deep learning: neural networks. And resolve only one problem via it: recognize the handwritten digits.

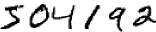
I will write code from scratch and talk about some math principles. But I will not spend much time on some details because its a brief tutorial. Programmers shall be able to fill in the gap.

01 Neural Nets

Neural Network is the model used in deep learning. We will begin from the concept of neuron.

how neuron works

A neuron or nerve cell is an electrically excitable cell that receives signals and make some response.

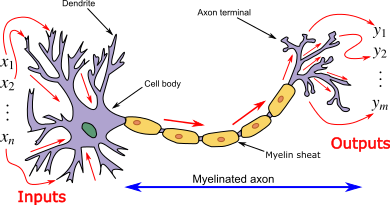
Deep learning make use of that structure to make some prediction.

perceptron

A perceptron takes several binary inputs and produces a single binary output.

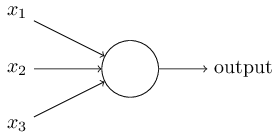
We can give its math description:

\[\begin{equation*} \mbox{output} = \begin{cases} 1 & \text{if } w\cdot x + b > 0 \\ 0 & \mbox{otherwise} \end{cases} \tag{1-1}\end{equation*}\]

The model tells how each input affects the output. (w stands for weight and b stands for bias.) The params w and b are what to “learn” from examples. With that, the model can predict new input. Do you know how to “learn” from the training data?

With the training data, we can make a small change \(\Delta w\) and \(\Delta b\) to make \(\|y - \hat{y}\|\) smaller. Then repeat the process until we get a good result. \(\hat{y}\) is the output and \(y\) is the actual value from training data.

However, this isn’t what happens when our network contains perceptrons. Perceptron is a “step function”, its output is a binary value. A small change \(\Delta w\) or \(\Delta b\) may make output jump from 0 to 1 or from 1 to 0. The “small change” is not possible for the output. It is not expected.

Sigmoid neurons

Sigmoid neurons is the solution for that.

\[\begin{eqnarray} \sigma(z) = \frac{1}{1+e^{-z}} \;\; and \;\; z = w \cdot x+b \tag{1-2}\end{eqnarray}\]

Its shape is a smoothed out version of a step function. And it makes the “small change” possible.